Suppose you want to describe to a friend exactly where the Sun is in the sky right now from your location on Earth. How would you go about it? What if you wanted to predict the time and location of sunrise? Or the exact moment when the Moon is fullest?

To answer these kinds of questions without literally pointing at the sky, we need to define some way to describe positions in the sky. Let’s imagine the sky as a hemisphere centered on our location, with its edge resting on the horizon around you. Using this hemisphere, we can label any position in the sky with two angles: (1) a compass direction (aka azimuth), and (2) a number of degrees above or below the horizon (aka altitude or elevation).

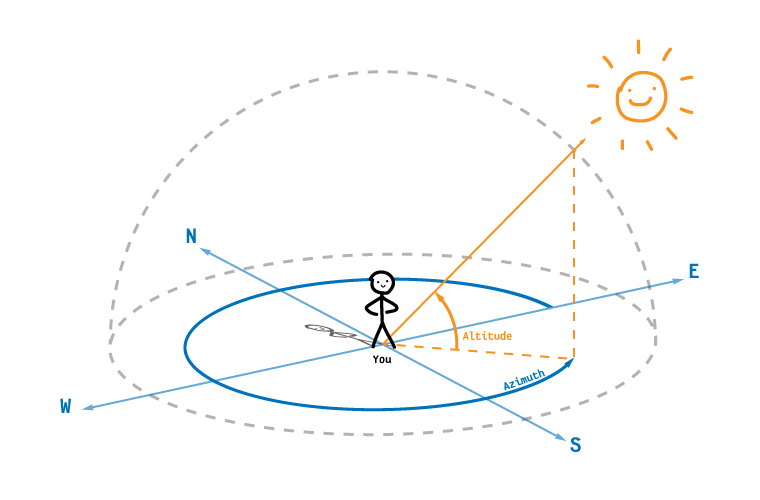
Having azimuth and altitude lets us describe positions in the sky, but accurately predicting the movements of celestial objects takes more consideration. To do this, let’s step back and consider the motion of objects around to the Sun.

Earth’s orbit traces out a ring around the Sun. If we fill in this ring to form a disc and extend that disc outwards to infinity it forms a plane. This plane containing the Earth and Sun is commonly called the ecliptic.

Using the ecliptic we can now describe any point in our Solar System! Basically: at a given time, a body (e.g. a planet or moon) will be some distance away from the Sun, at some angle around the Sun, and at some height above or below the ecliptic plane.

With these ecliptical coordinates, we can build a model to predict the location of celestial bodies. Many such models exist, relying on a host of features. These commonly include:

• Average distance to the Sun: often measured in “Astronomical Units”, aka “AU”. 1 AU is the average distance from the Earth to the Sun over one year.
• The shape of the orbit: through observation, we know that all planets in the solar system have elliptical orbits. Their exact distance from the sun varies as they move through space. We need parameters to describe the shape of each ellipse.
• The orientation of the orbit vs the ecliptic: the solar system is not flat! We need to know how the orbit is angled relative to the ecliptic.
• The place where the orbit crosses the ecliptic: aka an orbital node. These come in pairs: the ascending node is when an object passes up through the ecliptic, and the descending node is when that object passes back down through the ecliptic. By convention, “up” is typically the direction of the Earth’s North Pole.

Modeling lunar movements accurately requires some extra considerations. In particular, the Moon’s speed changes as it orbits the Earth. This happens in a few ways, largely having to do with gravitational effects from the Sun.

Combining these features, we can get a pretty good idea of where something is positioned in relation to the ecliptic. To get from here to a view of the sky from our own perspective, we need to establish one last coordinate system.

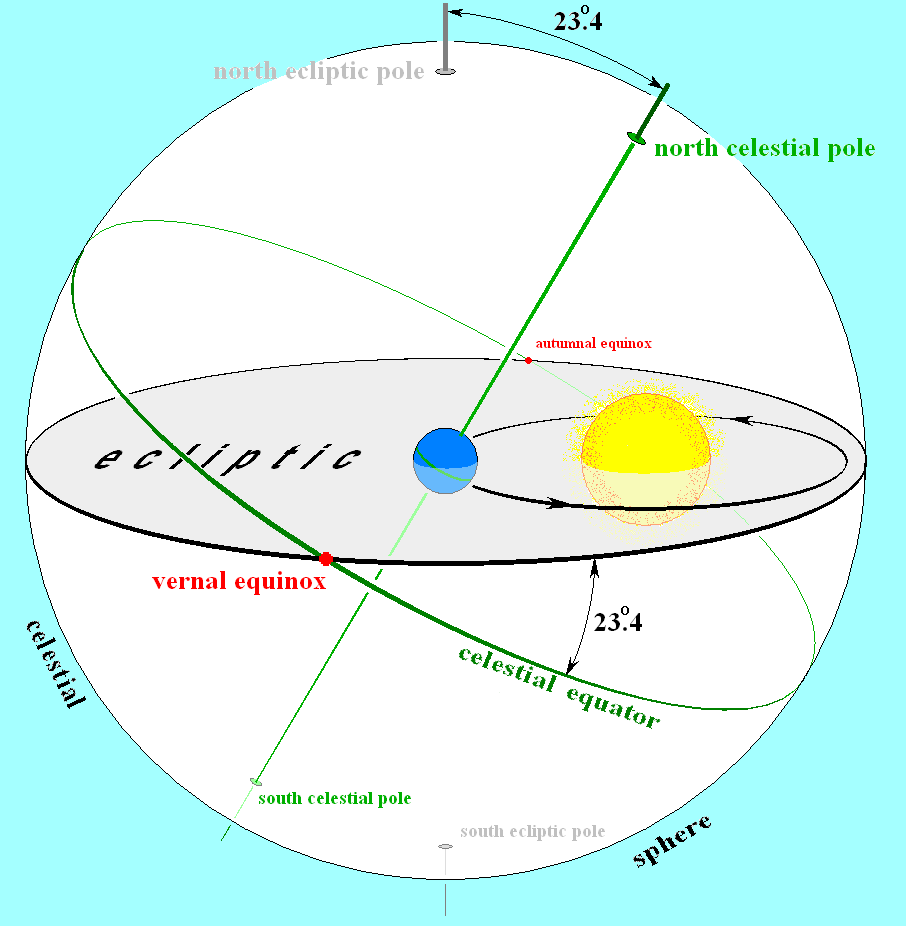
Imagine a sphere around the Earth, with its equator aligned with Earth’s equator. Let’s call this the celestial sphere. We can point at any position on the celestial sphere with two angles: the number of degrees around the equator (aka right ascension), and the number of degrees above or below the equator (aka declination). Conventionally, astronomical positions given in right ascension and declination are called ephemeris.

An ephemeris is sufficient to find events that happen at the same time globally, like equinoxes, moon phases, and eclipses.

Other events, like sunrise, sunset, or lunar transit (the moment the Moon passes overhead), require us to consider the perspective from a specific place on the Earth. We finally convert from a position on the celestial sphere to the azimuth and altitude coordinates on the hemisphere view of the sky defined earlier on.

This is accomplished using a location’s coordinates, given by latitude and longitude. There’s a lot to consider, but some big things that affect our local perspective of things include:

• Axial tilt: the Earth rotates around its axis once per day. That axis is tilted by 23.5-ish degrees.
• Earth’s movement through space: the Earth takes 24 hours to spin about its axis, but is also moving forward in its orbit during that time. As a result, it takes about 23 hours 56 minutes for objects (like stars) to appear in the same place in the sky. This period of time is called the sidereal day.
• Gravitational precession: because of its axial tilt, the Earth acts like a giant top. Its axis completes one cycle every 25,800 years. This is also known as a Great Year.

  

• Nutation: gravitational forces between the Earth, Moon, Sun, and other bodies act on Earth’s rotation, slightly changing the apparent location of objects in the sky
• Atmospheric refraction: When objects are low in the sky, they have to pass through more atmosphere, which distorts their appearance

Suntime makes use of all of the above (and more) to make accurate predictions about solar and lunar movements. If you’re interested in learning more about astrodynamics, I highly recommend checking out Bartosz Ciechanowski’s “Earth and Sun” post - it’s phenomenal. For more of the nuts and bolts of the calculations, I’ve referred to “Astronomical Algorithms” by Jean Meeus, “Calendrical Calculations” by Dershowitz and Reingold, and to Dr. Louis Strous’s “Astronomy Answers” website.

— Andrew